Geometry Unit 9 Answer Key

Prepare to delve into the captivating world of geometry with the Geometry Unit 9 Answer Key, your trusted companion on this mathematical journey. Dive into a comprehensive exploration of geometric concepts, theorems, and applications, unlocking the secrets of shapes, measurements, and transformations.

Let this guide be your beacon, illuminating the path to geometric mastery.

From the intricacies of coordinate geometry to the elegance of geometric constructions, this answer key unveils the hidden wonders of geometry. Discover the practical applications of geometric principles in architecture, engineering, and beyond, gaining a deeper appreciation for the power of geometry in shaping our world.

Geometry Unit 9 Concepts

Geometry Unit 9 delves into the fascinating world of circles, their properties, and their applications in various fields. Circles, defined by their constant distance from a fixed point called the center, are fundamental geometric shapes with a wide range of real-world applications.

Properties of Circles

Circles possess several unique properties that distinguish them from other geometric shapes. These include:

Radius:The distance from the center to any point on the circle.
Diameter:The distance across the circle through the center, equal to twice the radius.
Circumference:The distance around the circle, calculated as 2πr, where ris the radius.
Area:The amount of space enclosed within the circle, calculated as πr², where ris the radius.

Theorems and Proofs

Theorems are established facts in geometry that can be proven using axioms, definitions, and other theorems. Proofs are logical arguments that demonstrate the validity of theorems. Understanding theorems and proofs is crucial for developing a solid foundation in geometry.

Applying Theorems to Solve Geometry Problems

Theorems provide powerful tools for solving geometry problems. To apply a theorem, identify the relevant theorem and its conditions. Then, verify that the given problem satisfies the theorem’s conditions. Once you have established the applicability of the theorem, you can use it to deduce the desired conclusion.

Constructing Geometric Proofs

Constructing geometric proofs involves a step-by-step process that begins with stating the given information and the conclusion to be proven. Then, use known theorems, definitions, and logical reasoning to derive a series of statements. Each statement must follow logically from the previous ones until the conclusion is reached.

The key to constructing valid proofs is to ensure that every step is justified and the conclusion follows logically from the given information.

Measurement and Calculations

In geometry, measurement and calculations are crucial for determining the size, area, and volume of various geometric shapes. These calculations involve using specific formulas that provide accurate measurements.

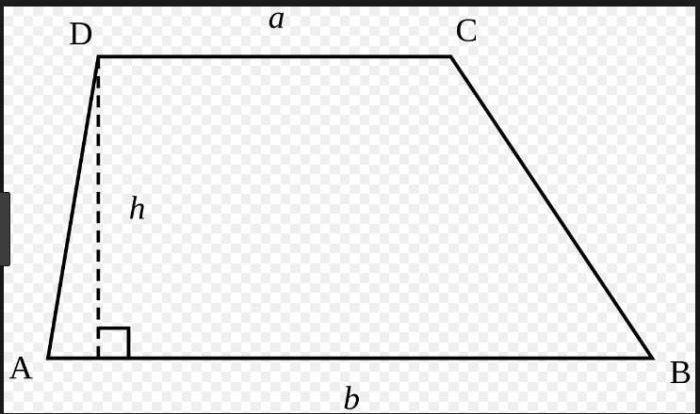
Area and Perimeter of 2D Shapes

Rectangle:Area = length × width, Perimeter = 2 × (length + width)
Square:Area = side², Perimeter = 4 × side
Triangle:Area = ½ × base × height, Perimeter = sum of all three sides
Circle:Area = πr², Circumference (Perimeter) = 2πr

Volume of 3D Shapes

Cube:Volume = side³
Cuboid:Volume = length × width × height
Sphere:Volume = (4/3)πr³
Cone:Volume = (1/3)πr²h
Cylinder:Volume = πr²h

Applications and Practice, Geometry unit 9 answer key

These formulas have practical applications in various fields, such as architecture, engineering, and construction. By understanding and applying these formulas, students can solve geometry problems related to measurement and calculations, including finding the area of a room, the volume of a container, or the perimeter of a garden.

Practice exercises and real-world examples can help students improve their measurement skills and develop a deeper understanding of geometric shapes.

Coordinate Geometry

Coordinate geometry, also known as analytic geometry, is a branch of mathematics that uses a coordinate system to represent geometric figures and solve problems involving them. It allows us to describe the position of points, lines, and other geometric objects using numerical coordinates.

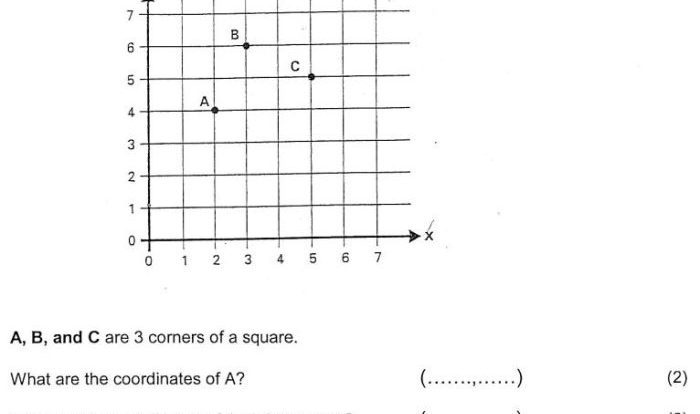
Plotting Points on a Coordinate Plane

A coordinate plane is a two-dimensional plane divided into four quadrants by two perpendicular lines called the x-axis and the y-axis. Each point on the plane is represented by an ordered pair of numbers (x, y), where x represents the horizontal distance from the origin (the point where the x-axis and y-axis intersect) and y represents the vertical distance from the origin.

Applications of Coordinate Geometry

Coordinate geometry has numerous applications in various fields, including:

Physics: Describing the motion of objects and analyzing forces
Engineering: Designing bridges, buildings, and other structures
Computer graphics: Creating 3D models and animations

li>Robotics: Programming robots to navigate and perform tasks

Geometric Shapes Represented Using Coordinate Geometry

Coordinate geometry can be used to represent various geometric shapes, such as:

Lines: Defined by equations of the form y = mx + b, where m is the slope and b is the y-intercept
Circles: Defined by equations of the form (x – h)^2 + (y – k)^2 = r^2, where (h, k) is the center and r is the radius
Parabolas: Defined by equations of the form y = ax^2 + bx + c
Ellipses: Defined by equations of the form (x – h)^2/a^2 + (y – k)^2/b^2 = 1
Hyperbolas: Defined by equations of the form (x – h)^2/a^2 – (y – k)^2/b^2 = 1

Transformations

Transformations are operations that move, flip, or turn geometric shapes without changing their size or shape. They play a crucial role in geometry, art, and various real-world applications.

There are three main types of transformations:

Translations

In a translation, a shape is moved from one point to another without changing its orientation.
To perform a translation, specify the direction and distance of the movement.
Translations are used in computer graphics, animation, and engineering to move objects.

Rotations

In a rotation, a shape is turned around a fixed point called the center of rotation.
To perform a rotation, specify the center of rotation and the angle of rotation.
Rotations are used in art, design, and engineering to create symmetrical patterns and shapes.

Reflections

In a reflection, a shape is flipped over a line called the line of reflection.
To perform a reflection, specify the line of reflection.
Reflections are used in art, architecture, and engineering to create mirror images and symmetrical designs.

Geometric Constructions: Geometry Unit 9 Answer Key

Geometric constructions are the processes of creating geometric shapes using only a compass and a straightedge. These tools allow us to create precise and accurate shapes without the need for complex calculations or measurements.

Some common geometric constructions include:

Bisecting an angle: Dividing an angle into two equal parts.
Constructing a perpendicular bisector: Creating a line that intersects a line segment at its midpoint and is perpendicular to it.
Constructing a circle: Creating a circle with a given radius.
Constructing a triangle: Creating a triangle with given side lengths or angles.

Geometric constructions are used in various fields, including architecture, engineering, and design. By understanding the steps involved in these constructions, you can create precise and accurate geometric shapes for your projects.

Problem-Solving Strategies

Problem-solving is a crucial aspect of geometry. Effective strategies can help students develop their critical thinking and problem-solving skills, enabling them to tackle various geometry problems with confidence.

Geometry problems often involve complex concepts and require a systematic approach. Understanding the problem, devising a plan, executing the plan, and reflecting on the solution are essential steps in problem-solving.

Tackling geometry unit 9? Don’t miss out on the answer key for extra support. While you’re at it, take a break and discover the intriguing Chinese herbal tea, huang lian wen dan tang . Its unique blend of herbs is said to promote well-being.

Afterward, return refreshed and ready to conquer geometry unit 9 with the answer key as your guide.

Identifying Problem Types

Common problem types in geometry include:

Proofs:Establishing the validity of geometric statements using logical reasoning.
Construction:Creating geometric figures using specific tools and techniques.
Measurement:Determining the length, area, volume, or angle measures of geometric figures.
Applications:Applying geometric concepts to solve real-world problems.

Problem-Solving Techniques

Effective problem-solving techniques include:

Understand the Problem:Read the problem carefully and identify the given information and what is being asked.
Draw a Diagram:Visualizing the problem can help clarify the situation and identify key relationships.
Break Down the Problem:Divide complex problems into smaller, manageable steps.
Use Logic and Reasoning:Apply geometric theorems, properties, and postulates to support your solution.
Check Your Solution:Verify your answer by substituting it back into the original problem or using a different method.

Examples

Consider the following problem:

Find the area of a triangle with a base of 10 cm and a height of 8 cm.

Using the problem-solving techniques mentioned above:

Understand the Problem:The problem asks for the area of a triangle given its base and height.
Draw a Diagram:Draw a triangle with a labeled base and height.
Break Down the Problem:The area of a triangle is given by the formula A = (1/2) – base – height.
Use Logic and Reasoning:Substitute the given values into the formula: A = (1/2) – 10 cm – 8 cm.
Check Your Solution:Calculate the area: A = 40 cm ². Verify that this answer makes sense given the dimensions of the triangle.

By applying effective problem-solving strategies, students can develop the skills necessary to tackle a wide range of geometry problems with confidence and accuracy.

Applications of Geometry

Geometry is not just a subject studied in classrooms; it is a fundamental tool used in various fields, from architecture to engineering to design. Geometric principles are applied to create structures, designs, and solutions that shape our world.

Architecture

Architects rely on geometry to design buildings, bridges, and other structures. Geometric shapes determine the strength, stability, and aesthetics of these structures. For instance, the use of triangles in bridges ensures their structural integrity under load.

Engineering

Engineers use geometry to design machines, vehicles, and other products. Geometric calculations help determine the optimal shapes and dimensions for efficiency and functionality. For example, the aerodynamic design of airplanes is based on geometric principles that minimize drag and improve fuel efficiency.

Design

Geometry is essential in graphic design, interior design, and product design. Geometric shapes and patterns create visual appeal, balance, and harmony in various designs. For instance, the use of the golden ratio in art and design is known to create aesthetically pleasing compositions.

Other Fields

Geometry also finds applications in fields such as robotics, computer graphics, and medicine. In robotics, geometric algorithms are used to control the movement and navigation of robots. In computer graphics, geometry is used to create 3D models and animations. In medicine, geometric imaging techniques, such as X-rays and CT scans, are used for diagnosis and treatment.

quinn

Geometry Unit 9 Answer Key